�S�����̗����̂�`��
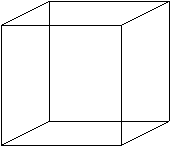
����͂�����ƍl����ƕs�\�Ȃ悤�ȋC�����܂��B�������A���̐}�͂R�����̗����̂ł����A
�Q�����̕��ʏ�ɕ`���Ă��܂��B����Ȃ�A�S�����̗����̂��A�Q�����̕��ʏ�ɕ`���Ă�����
��Ȃ��͂��ł��B
���̂Ƃ��A���ӂ��ׂ��́A���̐}�͗����̂��̂��̂ł͂Ȃ������̂̓��e�}���ƌ������Ƃł��B
�S�����̗����̂ɂ��Ă����l�ŁA�l����̂͂��̓��e�}�ł��B
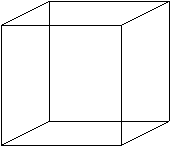 |
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�P
���ɁA�Q�����̗����̂͐����`�ł���ƍl���ėǂ��Ǝv���܂����A�Q�����̗����̂ƂR�����̗���
�̂̊W���l����Ǝ��̂悤�Ȑ}�ŕ\����܂��B
�@�@�@�@
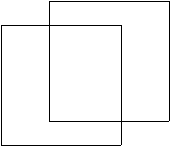 |
|||
 |
|||
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
![]() �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�A�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�A�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
 |
|||
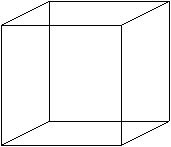 |
|||
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�B
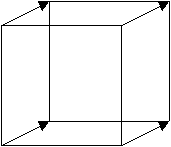
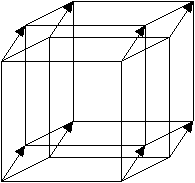
�@�@��ԓ��ŁA�����`���ړ�����B�ړ������͐����`���܂ޕ��ʂƐ����ȕ����ł��B
�A�@���̂Ƃ��̈ړ������́A���e�}��ł́A�����`�̏c�Ɖ��Ƃ͈قȂ�ߕ����ɕ`����邱�ƂɂȂ�܂��B
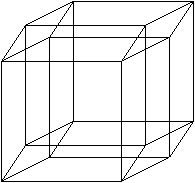
�B�@���̈ړ��ɂ����钸�_�̋O�Ղ�V���Ȑ����Ƃ��ĕt��������ƁA�R�����̗����̂��ł�������܂��B
�܂�A�R�����̗����̂́A�Q�����̗����́i�����`�j���������g�Ɛ����ȕ����Ɉړ������Ƃ��̋O��
�ɂȂ��Ă��܂��B
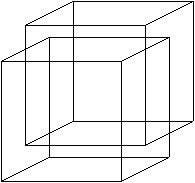
��ƑS�����l�ɂ��ĂR�����̗����̂����ɕ`�����Ƃ��ł�����̐}�`�����S�����̗����̂ƌĂԂׂ�
�}�`�̂͂��ł��B
 |
|||
 |
|||
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�C
![]()
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�D
 |
 |
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E
![]()
�C�@�S������ԓ��ŁA�R���������̂��ړ�����B�ړ������͂R���������̂��܂ނR������ԂƐ����ȕ�����
����B
�D�@���̂Ƃ��̈ړ������́A���e�}��ł́A�R���������̂̏c�Ɖ��Ɖ��s���Ƃ͈قȂ�ߕ����ɕ`�����
���ƂɂȂ�B
�@ �E�@���̈ړ��ɂ����钸�_�̋O�Ղ�V���Ȑ����Ƃ��ĕt��������ƁA�S�����̗����̂��ł�������B
�@�l���Ă݂�ƁA�_����o�����Đ����A�����`�E�E�E�Ƃ��̂悤�ɂ��ďo���オ��̂��ƌ������Ƃ��ł��܂��B
�@�@�����āA�T�����A�U�����̗����̂̐}���������@�ŕ`�����Ƃ��ł��܂��B
![]() �E�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�@�@�@�@�@�@�@�E�@�@�@�@�@�@�@�@
�E�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�@�@�@�@�@�@�@�E�@�@�@�@�@�@�@�@
 |
|||||||||||
 |
|||||||||||